Verichains at HITBxPHDays Bangkok: Demystifying the Critical “Proof Forgery Attack” on zkEVM
This May, we made a return to Hack in the Box (HITB) Security Conference, took center stage at HITBxPHDays Bangkok, to delve deeper into this critical find. Our presentation transcended a specific exploit, delving deeper into the inherent risks associated with optimizing cryptographic protocols, particularly for emerging technologies like zero-knowledge proofs (ZKPs) and multi-party computation (MPC).
Trusted Centralized Components is a Recipe for Disaster
While the concept of a single, trusted component controlling a blockchain network might initially appear attractive – offering a potential defense against widespread attacks – it fundamentally undermines the core nature of blockchain – decentralization. In that situation, a successful compromise of this central authority would cripple the entire network.
Under the hood of zkEVM
Zero-Knowledge Proofs (ZKPs) have emerged as a game-changer in the blockchain space, offering significant scalability advantages. However, as they are relatively new, it necessitates a heightened focus on potential security risks. Our presentation at HITBxPHDays Bangkok addressed these very concerns, delving into the hidden complexities and vulnerabilities that could be exploited by malicious actors.
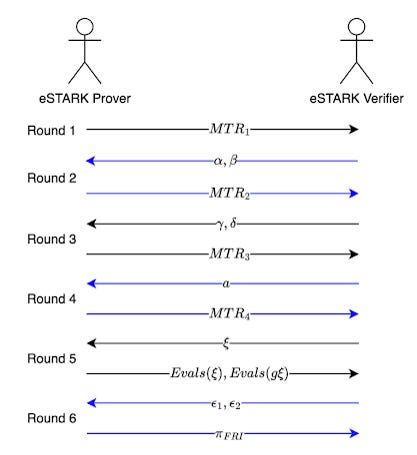
To provide a more solid foundation for understanding these vulnerabilities, the presentation commenced with a detailed breakdown of zkEVM. We then explored the intricacies of its underlying cryptographic protocol, specifically the 6 rounds of the eSTARK prover algorithm and 4-step verifier algorithms.
eSTARK Prover Algorithm
Round 1: Commit Trace Column Polynomials tri ∈ 𝔽<n[X], where 𝔽 = 𝔽p, p = 264 - 232 + 1.
Round 2: Extract challenges α, β ∈ 𝕂, compute and commit Inclusion Polynomials hi,1, hi,2 ∈ 𝕂<n[X], where 𝕂 = 𝔽p^3.
Round 3: Extract challenges γ, δ ∈ 𝕂, compute and commit Grand Product Polynomials Zi ∈ 𝕂<n[X] (and Intermediate Polynomials imi ∈ 𝕂[X]).
Round 4: Extract challenge a ∈ 𝕂, compute Quotient Polynomial Q ∈ 𝕂<2n[X]. Split Q into smaller polynomials Qi ∈ 𝕂<n[X] and commit Qi. Note that C(X) represents preprocessed polynomials and committed polynomials, and ZH(X) is the vanishing polynomial over Evaluation Domain H.
Round 5: The prover extracts the challenge ξ ∈ 𝕂 and provides necessary evaluations of the committed polynomials at ξ and gξ, denoted as Evals(ξ), Evals(gξ). These Evals must satisfy the following condition.
Round 6: The prover extracts the challenges ϵ1, ϵ2 ∈ 𝕂 and constructs the batched FRI polynomial F ∈ 𝕂<n[X]. Run the batched FRI protocol on F to obtain FRI proof πFRI, which implies that Evals(ξ), Evals(gξ) are all correct.
eSTARK Verifier Algorithm
Check that Merkle roots and each element in Evals(ξ), Evals(gξ) are all in 𝕂.
Compute Fiat-Shamir challenges from eSTARK proof πeSTARK.
Check that all constraints are satisfied at ξ from Round-5 evaluations.
Run FRI verification on πFRI to ensure that all Round-5 evaluations are correct.
Furthermore, we discussed the potential risks associated with the optimization approach of combining STARK for proving and SNARK for verification in the Proof Recursion step. While this technique aims for efficiency, it can introduce unnecessary complexities if not implemented with meticulous care. With Proof Forgery Attack, we can fake a “valid” πrecf without knowing πbatch, the eSTARK proof for one batch of valid transactions. Once obtaining πrecf, the attacker can proceed with the protocol and forge the final zkEVM proof πfflonk.
A Vulnerability Lurking in the Shadows
Verichains researchers unearthed a critical vulnerability within a zkEVM system. This stemmed from a fundamental incompatibility between the mathematical foundations of STARK and SNARK utilized by the system. Specifically, the system attempted to reconcile elements from the STARK prover over 𝕂 = 𝔽p^3 (192-bit entropy), with the SNARK verification circuit over 𝔽q (254-bit entropy), where q is a 254-bit prime number, tied to a pairing-friendly elliptic curve group supported by Ethereum and SNARK fflonk, namely BN128.
By carefully performing security assessment, Verichains identified two weaknesses in the recursiveF sub-processes. One is in the Merkle leaf hashing circuit “linearhash”, where three 64-bit elements are linearly combined into one 192-bit element, via the map (x,y,z) → x + 264y + 2128z, but there’s no constraints to check if each of these elements is from the field 𝔽p. The second weakness arises in the “multiply-then-add” operation, which takes three input a, b, c ∈ 𝕂 and outputs an element (a*b + c) of 𝕂. Given that a*b is roughly 128-bit long before doing the modulo reduction, as a result, the third operand c, is allocated more space than necessary.
This incompatibility exposed a significant security flaw: the potential to forge valid proofs for any computation within the network. Such a feat would empower attackers to manipulate the entire system at will, enabling them to steal funds or even halt transactions entirely. The most concerning aspect, however, lay in the inherent anonymity afforded by the zero-knowledge nature of zkEVM. An attack of this nature would be completely undetectable, leaving no trace for forensic analysis.
To underscore the potential ramifications, Verichains team at HITBxPHDays Bangkok also presented live demonstrations showcasing two distinct scenarios where a malicious actor could exploit this vulnerability and wreak havoc on the network.
Forging zkEVM proof by cracking Merkle Commitment Scheme & Remediation
Suppose we want to Merkle commit f(hi) = (0,0,0), with hi from the Evaluation Domain H = {h1, h2,… , hm}. By leveraging the two weaknesses, we can maliciously reveal f(hi) to be (x,y,z) instead of (0,0,0). We have two relations in three variables (a,b,c) corresponding to vulnerable “multiply-then-add” and “linearhash” functions, respectively.
(a,b,c) = (x,y,z) mod p
a + 264b + 2128c = 0 mod q
Using the above method, we have the strategy to crack eSTARK protocol as follows:
Round 1 to Round 4: As we do not have polynomials representing the correct execution, we can commit all polynomials as zeroes.
Round 5: Deduce a tuple (x,y,z) for Q(ξ) instead of (0,0,0). Reveal Q1 and Q2 at ξ as (x1,y1,z1) and (x2,y2,z2), other evaluations as (0,0,0).
Round 6: Run the FRI protocol as normal. In the FRI query phase, reveal evaluations of Q1 and Q2 as (a1,b1,c1) and (a2,b2,c2).
Given Q(ξ) = (x,y,z) and challenge ξ ∈ 𝕂, we have five relations in 12 variables (x1,y1,z1), (x2,y2,z2), (a1,b1,c1) and (a2,b2,c2). To find solutions for the following system of modular linear equations, an effective approach is to employ Lattice Reduction, which aids in identifying small solutions.
(x1,y1,z1) + ξn(x2,y2,z2) = (x,y,z) over 𝔽p^3
(a1,b1,c1) = (x1,y1,z1) mod p
(a2,b2,c2) = (x2,y2,z2) mod p
a1 + 264b1 + 2128c1 = 0 mod q
a2 + 264b2 + 2128c2 = 0 mod q
With a “valid” πeSTARK, one can just simply follow the rest of the protocol to forge the final zkEVM proof. Note that the final zkEVM proof is a fflonk proof, which contains completely random numbers; no one can tell how it is forged since the mechanism is completely hidden by the zero-knowledgeness of the argument systems.
By leveraging this strategy, the attacker gains the ability to manipulate the state change, thereby enabling them to potentially immobilize the assets within the network or manipulate the state to a specific value, granting exclusive knowledge to the attacker on how to withdraw funds.
Following Verichains' disclosure, the team conducted an exhaustive review to fully grasp the vulnerability's dynamics and implications. The following summarizes the adjustments made to pil-stark, as validated by the Verichains team:
GL value constraints: Added constraints to ensure that all inputs to the recursiveF verifier circuit are below 264. These were incorporated into the StarkVerifier BN128 template.
GL operations: Introduced new templates for additions and subtractions within the BN128 field, named GLSub (and GLCSub), and GLAdd (andGLCAdd). Additionally, operations for multiplication and addition were segregated, eliminating the use of GLCMulAdd for query or evaluation verifications.
GL operation tags: New tags were added to the recursiveF verifier circuit for more precise constraint application during GL operations in the BN128 field. A tag, {maxNum}, denotes the maximum possible signal value, set at p – 1, with p = 0xFFFFFFFF00000001.
Testing: Adjustments were made to accommodate tags in tests. Two new tests were devised to probe edge cases in VerifyEvaluations and VerifyQuery, ensuring tags are correctly applied. One test challenges the template with maximum input values (p – 1), while the other modifies the template to maintain tag values without performing subtraction.
Links to the fix:
The Importance of Security for ZKP Implementation
We have explored ZKPs and MPC’s potential to revolutionize blockchain, but we need to be cautious about how we optimize and implement them. Security is paramount, especially when dealing with new and cutting-edge technologies. Here are our key takeaways for a safer and more efficient optimization for cryptographic protocols.
Avoid centralized components: Blockchains are supposed to be decentralized, so relying on a single trusted entity is a big no-no.
ZKPs and MPC are new and complex: These powerful tools come with hidden risks. Every line of code needs careful scrutiny.
Security audits are essential: Regular audits by security experts are crucial for identifying and patching vulnerabilities before they can be exploited.
Collaboration is key: Developers and security experts need to work together to build truly secure cryptographic systems.